scs
Syntax
scs(f, [P], [A], [b], [Aeq], [beq], [lb], [ub], [x0], [c], [eps],
[alpha])
Details
Solve the following optimization problem for the objective function with given constraints:
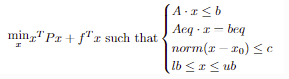
The result is a 2-element tuple. The first element is the minimum value of the objective function. The second element is the value of x when the value of the objective function is minimized.
Parameters
f is a vector of coefficients for linear terms in the quadratic programming problem. It must be of the same length as x0.
P (optional) is a matrix obtained by multiplying the diagonal elements of the coefficient matrix for quadratic terms by 2. For example, to obtain matrix p, form an upper triangular matrix based on all the quadratic terms:

A (optional) is a coefficient matrix for linear inequality constraints. Its number of columns must be consistent with the size of x.
b (optional) is the right-hand vector for linear inequality constraints.
Aeq (optional) is a coefficient matrix for linear equality constraints. Its number of columns must be consistent with the size of x.
beq (optional) is the right-hand vector for linear equality constraints.
lb / ub (optional) is a scalar or a vector of the same length as x, specifying the lower/upper bounds for variables.
-
If lb or ub is a scalar, all variables are subject to the same lower or upper bound constraints. If lb or ub is null, there are no lower or upper bound constraints for x.
-
If lb or ub is a vector, the elements of x are subject to the corresponding elements of lb or ub. If a certain element in lb or ub is null, the corresponding element in x has no lower or upper bound constraint.
x0 (optional) is a vector of coefficients for absolute value inequality constraints.
c (optional) is a non-negative number representing the right-hand constant for absolute value inequality constraints.
eps (optional) is a positive floating-point number representing the solution precision. The default value is 1e-6, and the range is [1e-4, 1e-9]. A solution with higher precision can be obtained by decreasing eps. If a value beyond the range is set, it will be adjusted to the default value.
alpha (optional) is a positive floating-point number representing the relaxation parameter. The default value is 1.5, and the range is (0,2). The solution process can be sped up by increasing alpha. If a value beyond the range is set, it will be adjusted to the default value.
Examples
Find x and y that satisfy the following constraints and minimize the objective function x2 + y2:

// No linear terms in the objective function, so all coefficients are 0, and f takes the following values
f = [0, 0];
// Only quadratic terms x^2 and y^2 exist with coefficients as 1, so p takes the following values
P = [2, 0, 0, 2]$2:2;
// Coefficients and right-hand vector for absolute value inequality constraints
x0 = [0.4, 0.6];
c = 0.5;
// Linear equality constraint x + y = 1, so Aeq and beq take the following values
Aeq = [1, 1]$1:2;
beq = [1];
// Since x, y > 0, we have lower bounds for variables as follows:
lb = [0, 0];
re = scs(f=f,P=P,Aeq=Aeq,beq=beq,lb=lb,x0=x0,c=c);
re[1]
// output: [0.500000043984074,0.499999955746447]