quadprog

quadprog(H, f, [A], [b], [Aeq], [beq])

H, A and Aeq must be matrices with the same number of columns.

f, b and beq are vectors.

A is the coefficient matrix of linear inequality constraints.

b is the right-hand-side vector of the linear inequality constraint.

Aeq is a linear equality constraint coefficient matrix.

beq is the right-hand-side vector of the linear equality constraint.

Solve the following optimization problem with a quadratic objective function and a set of linear constraints.

The result is a 2-element tuple. The first element is the minimum value of the objective function. The second element is the value of x where the value of the objective function is minimized.

Example 1: Find the minimum of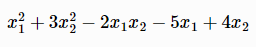

H=matrix([2 -2,-2 6])
f=[-5,4]
x=quadprog(H,f);

x[0];
// output
-6.375

x[1];
// output
[2.75,0.25]

Example 2: Find the minimum of

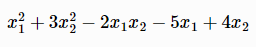
subject to the constraints of

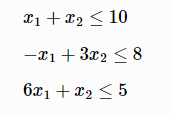
H=matrix([2 -2,-2 6])
f=[-5,4]
A=matrix([1 -1 6, 1 3 1])
b=[10, 8, 5]
x=quadprog(H,f,A,b);

x[0];
// output
-4.092975

x[1];
// output
[0.904959, -0.429752]

Example 3: Find the minimum of

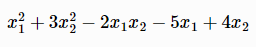
subject to the constraints of

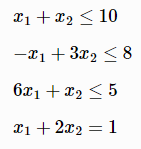
H=matrix([2 -2,-2 6])
f=[-5,4]
A=matrix([1 -1 6, 1 3 1])
b=[10, 8, 5]
Aeq=matrix([1],[2])
beq=[1]
x=quadprog(H,f,A,b,Aeq,beq);

x[0];
// output
-3.181818

x[1];
// output
[0.818182,0.090909]

The 3 examples above share the same objective function. Example 1 has no constaints and achieves the lowest minimum value. Example 3 has more constaints than example 2 and therefore can only achieve a higher minimum value than both example 2 and example 1.