qclp
Syntax
qclp(r, V, k, [A], [b], [Aeq], [beq], [x0], [c], [eps], [alpha])
Parameters
V, A and Aeq must be matrices with the same number of columns.
r, b and beq are vectors.
k is a positive scalar.
x0 is a vector of coefficients for absolute value inequality constraints.
c is a non-negative number representing the right-hand constant for absolute value inequality constraints.
eps is a positive floating-point number representing the solution precision. The default value is 1e-6, and the range is [1e-4, 1e-9]. A solution with higher precision can be obtained by decreasing eps. If a value beyond the range is set, it will be adjusted to the default value.
alpha is a positive floating-point number representing the relaxation parameter. The default value is 1.5, and the range is (0,2). The solution process can be sped up by increasing alpha. If a value beyond the range is set, it will be adjusted to the default value.
Details
Solve the following optimization problem with a linear objective function and a set of constraints including a quadratic constraint.
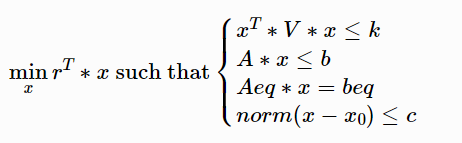
The result is a 2-element tuple. The first element is the minimum value of the objective function. The second element is the value of x where the value of the objective function is minimized.
Examples
Determine the optimal portfolio based on expected average returns (r) and the variance-covariance matrix (V) of selected stocks, and the constraints that the volatility of the portfolio should be no more than 11% and the weight of each stock in the portfolio is between 10% and 50%.
r = 0.18 0.25 0.36
V= 0.0225 -0.003 -0.01125 -0.003 0.04 0.025 -0.01125 0.025 0.0625 $ 3:3
k = pow(0.11, 2)
A = (eye(3) join (-1*eye(3))).transpose()
b = 0.5 0.5 0.5 -0.1 -0.1 -0.1
Aeq = (1 1 1)$1:3
beq = [1]
x = qclp(-r, V, k, A, b, Aeq, beq);
x[1];
// output: [0.5,0.176297,0.323703]Based on the above example, adding absolute value constraints | x1 - 0.35| + | x2 - 0.35 | + | x3 - 0.35 | ≤ 0.3 :
x0 = [0.35, 0.35, 0.35];
c = 0.3;
y = qclp(-r, V, k, A, b, Aeq, beq, x0, c);
y[1]
// output: [0.475001,0.247962,0.277037]