linprog
Syntax
linprog(f, [A], [b], [Aeq], [beq], [lb], [ub],
[method='simplex'])
Details
Solve the following optimization problem with a linear objective function and a set of linear constraints.
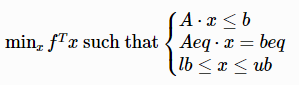
The result is a 2-element tuple. The first element is the minimum value of the objective function. The second element is the value of x where the value of the objective function is minimized.
Parameters
A and Aeq must be matrices with the same number of columns.
f, b and beq are vectors.
-
If lb or ub is a scalar, all elements of x are subject to the same lower bound or upper bound constraint.
-
If lb or ub is null, there is no lower bound or upper bound constraint for x.
-
If lb or ub is a vector, an element of x is subject to the lower bound or upper bound constraint specified by the corresponding element of lb or ub.
method is a string indicating the optimization algorithm. It can be either 'simplex' (recommended) or 'interior-point'.
Examples
Example 1. Find the minimum of x+2y subject to the constraints of
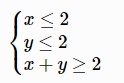
f = [1, 2];
A = [-1, -1]$1:2;
b = [-2];
ub = 2;
re = linprog(f, A, b, , , , ub);
re[0];
// output: 2
re[1];
// output: [2,0]Example 2. Find the minimum of -3x1-2x2 subject to the constraints of
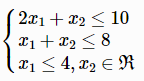
f = [-3, -2];
A = [2, 1, 1, 1]$2:2;
b = [10, 8];
ub = [4, NULL];
re = linprog(f, A, b, , , , ub);
re[0];
// output: -18
re[1];
// output: [2,6]