socp

socp(f, [G], [h], [l], [q], [Aeq], [beq])

Second-order cone programming (SOCP) problems are subject to the constraint with the following form:

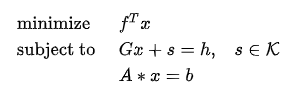
K is a cone and s is a slack variable. The value of s will be determined during optimization.

f is a numeric vector indicating the coefficient vector of the objective function.

G (optional) is a numeric matrix indicating the coefficient matrix of the cone constraint.

h (optional) is a numeric vector indicating the right-hand-side vector of the cone constraint.

l (optional) is an integral scalar indicating the dimension of the non-negative quadrant constraint.

q (optional) is a positive vector indicating the dimension size of each second-order cone constraint. The form is [r0,r1,…,rN-1].

Aeq (optional) is a numeric matrix indicating the coefficient matrix of the equality constraint.

beq (optional) is a numeric vector indicating the right-hand-side vector of the equality constraint.

Solve SOCP problems and calculate the minimum of the objective function under specified constraints. The standard form of the SOCP constraint is as follows:

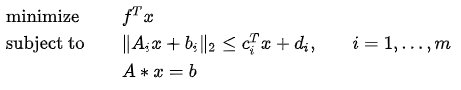
G is as follows:

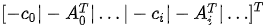
h is as follows:

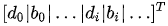
Return value: A 3-element tuple:

• The first element is a string indicating the state of the solution:

  • Problem solved to optimality: optimal solution found;

  • Found certificate of primal infeasibility: no feasible solution to the primal;

  • Found certificate of dual infeasibility: no feasible solution to the dual;

  • Offset exitflag at inaccurate results: inaccurate results;

  • Maximum number of iterations reached: reach the maximum number of iterations;

  • Search direction unreliable: unreliable search direction;

  • Unknown problem in solver: the solver cannot identify the problem.

• The second element is the value of x where the value of the objective function is minimized.

• The third element is the minimum value of the objective function.

Solve the following SOCP problem:

f = [-6, -4, -5]
G = matrix([[16, 7, 24, -8, 8, -1, 0, -1, 0], 
[-14, 2, 7, -13, -18, 3, 0, 0, -1], 
[5, 0, -15, 12, -6, 17, 0, 0, 0]])
h = [-3, 5, 12, -2, -14, -13, 10, 0, 0]

l = 2
q = [4,3]

re = socp(f,G,h,l,q, ,)
print(re)

// output > ("Problem solved to optimality",[-9.902804882871327,-1.39084684264198,26.211851780740154],-66.079042235904907)