A Guide to SOCP: From Problem Formulation to Solution
In quantitative finance, optimization solvers are essential tools for tackling complex decision-making problems in portfolio optimization, risk assessment, and asset pricing. DolphinDB's suite of optimization solver functions - including linprog, quadprog, qclp, and socp - enables practitioners to translate financial problems into mathematical models and find optimal solutions.
Among these, the socp function (for second-order cone programming
problems) is particularly effective for handling uncertainty and nonlinear constrains.
In risk management, it efficiently handles quadratic constraints, such as those
involving variance and standard deviation calculations. In portfolio
optimization, it manages various market complexities, such as leverage limits,
market exposure constraints, and capital requirements. Additionally, the
socp function demonstrates superior computational efficiency when
handling large datasets, allowing it to quickly converge to globally optimal
solutions.
This article provides a comprehensive introduction to the socp function
in DolphinDB, using a practical portfolio optimization example to demonstrate how
real-world financial problems can be reformulated and solved with the SOCP problem.
1. Mathematical Model of SOCP Problems
The socp function is used to solve Second-Order Cone Programming
(SOCP) problems, which are highly versatile and applicable in a wide range of
scenarios. While DolphinDB provides specialized functions for specific optimization
types like Linear Programming (LP), Quadratic Programming (QP), and Quadratically
Constrained Linear Programming (QCLP), these problems can alternatively be solved
using the socp function by reformulating them into SOCP format (see Section 3).
To better understand the socp function and how to transform
optimization problems into SOCP form, we will first introduce the mathematical model
of SOCP and explain which types of optimization problems it can address.
1.1 Cone Representation of SOCP Problems
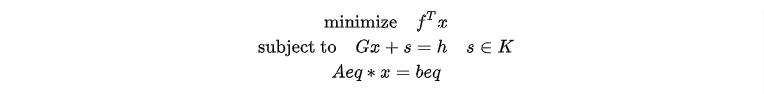
where,
-
K is the cone.
-
s is a slack variable whose value is determined during optimization.
-
f is a numerical vector indicating the coefficient vector of the objective function.
-
G is a numerical matrix indicating the coefficient matrix of the cone constraints.
-
h is a numerical vector indicating the right-hand side of the cone constraints.
-
Aeq is a numerical matrix indicating the coefficient matrix of the equality constraints.
-
beq is a numerical vector indicating the right-hand side of the equality constraints.
The equation Gx+s=h encompasses all inequality constraints in an SOCP problem, including both linear inequalities and second-order cone constraints. The problem's dimensions are defined by two key parameters of the socp function: l and q. l is an integer that specifies the dimension of the non-negative orthant constraints, i.e., the dimension of the linear inequalities. q is a positive vector in the form [r0, r1,…, rN-1], which contains the dimensions for each second-order cone constraint. Note that each dimension in q should be incremented by 1, accounting for both the 2-norm term on the left-hand side and the scalar term on the right-hand side of the inequality. Thus, the total l+sum(q) should equal the number of rows in matrix G.
1.2 Standard form of SOCP Problems
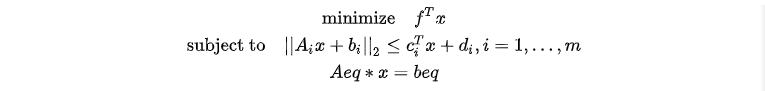
The standard form of an SOCP problem can be transformed into the cone form
described above, allowing us to determine the corresponding parameters G,
h, l, and q of the socp function for
solving the problem. Below, we explain how to derive the cone form from the
standard form to provide a clearer understanding.
1.Refomulate the second-order cone constraints
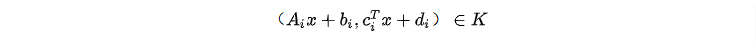
2.Combine these constraints and introduce an auxiliary variable s
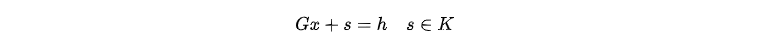
The resulting forms of G and h are as follows:
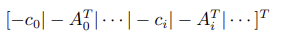
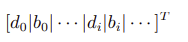
2. Converting Programming Problems to SOCP Form
The conversion of general programming problems to SOCP requires transforming the original problem into SOCP standard form by constructing appropriate parameters based on the relationship between cone representation and standard form.
2.1 SOCP Form of Linear Programming
A linear programming problem involves optimizing a linear objective function subject to linear constraints. Its form is as follows:
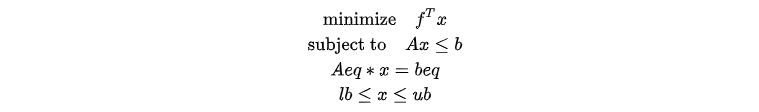
For problems with linear inequality constraints 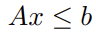 , we can rearrange terms for
, we can rearrange terms for 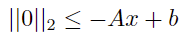 .
.
For the linear constraints of the variable x, upper and lower bounds 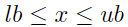 can be converted to
can be converted to
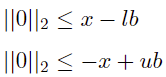
Standard SOCP form:
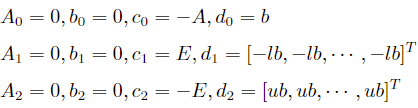
Where E is an identity matrix of the same dimension as x.
Construct the parameters:

2.2 SOCP Form of Quadratic Inequality Constraints
A quadratically constrained linear problem involves optimizing a linear objective function subject to constraints that contain quadratic terms. Its form is as follows:
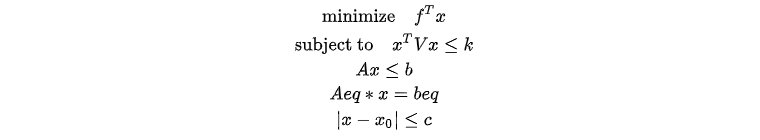
For quadratic inequality constraints ![]() where V is a positive definite matrix and k is a positive
scalar. V can be decomposed using Cholesky decomposition into V =
FTF. The original constraint can then be transformed:
where V is a positive definite matrix and k is a positive
scalar. V can be decomposed using Cholesky decomposition into V =
FTF. The original constraint can then be transformed:
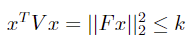
Standard SOCP form:
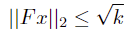
Construct the parameters:
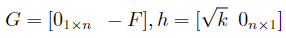
Where n indicates the length of variable x.
2.3 SOCP Form of Absolute Value Constraints
An absolute value constrained problem involves optimizing a linear objective function subject to linear constraints, with some constraints containing absolute values. Its form is as follows:
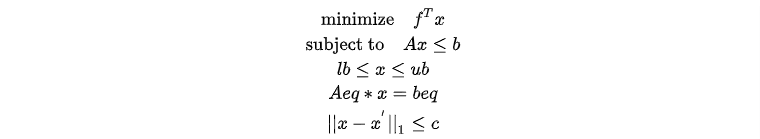
The 1-norm constraints can be expressed as the absolute value constraints.
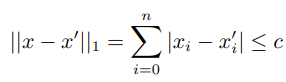
By introducing auxiliary variable ui
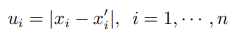
We can rewrite the problem in terms of the vector [xT, u1, ··· , un]T and convert it into the SOCP form.
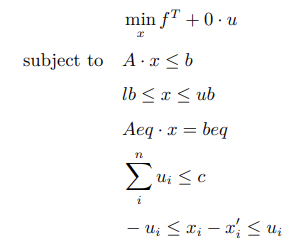
Construct the parameters:
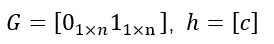
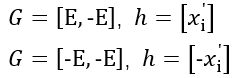
2.4 SOCP Form of Quadratic Programming
A quadratic programming problem involves optimizing a quadratic objective function subject to linear constraints. Its form is as follows:
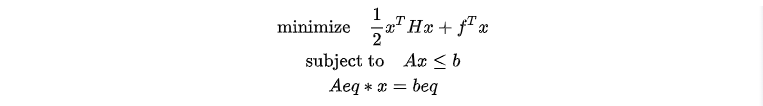
For such problems, we can introduce an auxiliary variable y = xTHx, where H is a positive definite matrix. Through Cholesky decomposition, H can be decomposed into H = UTU. By applying the parallelogram identity, the problem can be transformed to:
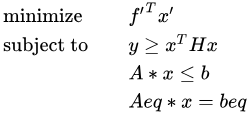
Second-order cone constraints:
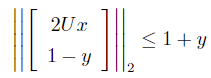
Standard SOCP form:
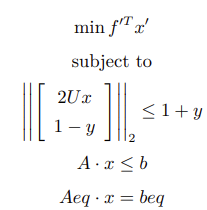
Where
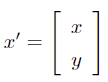
Construct the parameters:
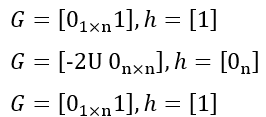
3. Use Cases
In this section, we will explore two portfolio optimization cases that illustrate how
to reformulate financial problems into the SOCP format. Through these examples,
we'll demonstrate step-by-step how to use the socp function to
obtain optimal solutions.
3.1 Portfolio Optimization: with Linear Programming
This case demonstrates how to reformulate a linear stock portfolio optimization problem into SOCP format. The objective is to maximize expected returns while satisfying multiple weight constraints.
3.1.1 Mathematical Model
The problem can be transformed into a mathematical model with the objective function as follows:
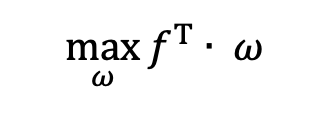
Where:
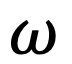 is target weight of each stock
in the portfolio
is target weight of each stock
in the portfolio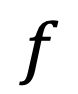 is expected return of each stock
in the portfolio
is expected return of each stock
in the portfolio
The model includes the following constraints for:
- Individual stock weight
- Component stock weight
- Deviation for component stock weights
- Market capitalization weight
- Industry weight
- Prohibition of investing in certain stocks
- Target stock weights
Specifically:
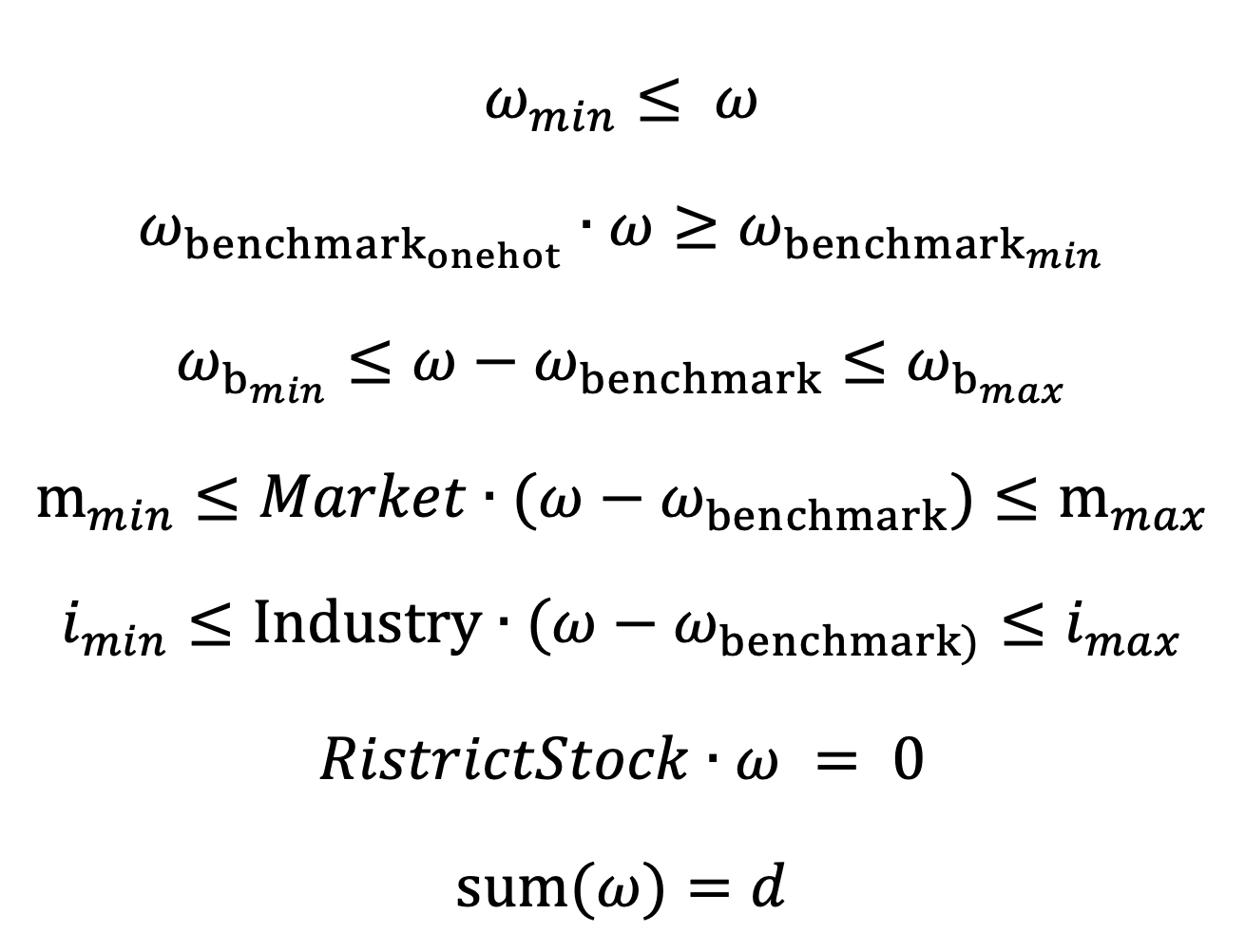
3.1.2 Defining Parameters
The syntax of the socp function is socp(f, [G], [h],
[l], [q], [A], [b]). Below are the steps to define the
parameters.
Coefficient vector of the objective function (f):
Since the socp function minimizes the objective function by
default, negate the original expected returns:
f_1 = -fCoefficient matrix for cone constraints (G):
unit_matrix = eye(vector_size)//vector_size is the number of stocks in portfolio
G = concatMatrix([-unit_matrix, -transpose(matrix(w_b_onehot))], false) // individual stock weight and component stock weight
G = concatMatrix([G, unit_matrix], false) // component stock deviation <max>
G = concatMatrix([G, -unit_matrix], false) // component stock deviation <min>
G = concatMatrix([G, transpose(matrix(market_vector))], false) // market capitalization weight <max>
G = concatMatrix([G, -transpose(matrix(market_vector))], false) // market capitalization weight <min>
G = concatMatrix([G, transpose(matrix(industry_matrix))], false) // industry weight <max>
G = concatMatrix([G, -transpose(matrix(industry_matrix))], false) // industry weight <min>Right-hand-side vector for cone constraints (h):
h = array(DOUBLE).append!(w_min) // individual stock weight
h.append!(-w_b_t_min) // component stock weight
cs_max_temp = w_b_max + w_b // component stock deviation <max>
h.append!(cs_max_temp)
cs_min_temp = -w_b_min - w_b // component stock deviation <min>
h.append!(cs_min_temp)
mk_max_temp = m_max + transpose(matrix(market_vector))**w_b // market capitalization weight <max>
h.append!(mk_max_temp[0])
mk_min_temp = -m_min - transpose(matrix(market_vector))**w_b // market capitalization weight <min>
h.append!(mk_min_temp[0])
ind_max_temp = ind_max + transpose(matrix(industry_matrix))**w_b // industry weight <max>
h.append!(ind_max_temp[0])
ind_min_temp = -ind_min - transpose(matrix(industry_matrix))**w_b // industry weight <min>
h.append!(ind_min_temp[0])Dimension of non-negative orthant constraints (l): As all constraints are linear, l equals the size of h:
l = h.size() Dimension size of second-order cone constraints (q): As there are no second-order cone constraints in this example, q is set to an empty vector.
q = []Coefficient matrix and right-hand-side vector for equality constraints (Aeq and beq):
one_vector = matrix(DOUBLE, 1, vector_size, , 1)
Aeq = concatMatrix([one_vector, transpose(matrix(restrict_stock))], false) // target stock weight and prohibited stock
beq = array(DOUBLE).append!(d) // target stock weight
beq.append!(0) // prohibited stock3.1.3 Solving the Optimization Problem
Invoke the socp function with the defined parameters:
res = socp(f_1, G, h, l, q, Aeq, beq)3.2 Portfolio Optimization: with Turnover Constraints and Tracking Error Constraints
This case extends the MVO (Mean-Variance Optimization) model to optimize a portfolio by balancing return maximization and risk minimization. It introduces additional constraints, including turnover constraints (limit portfolio rebalancing costs) and tracking error constraints (limit the portfolio's volatility relative to the benchmark), alongside those from the previous example.
3.2.1 Mathematical Model
The problem can be transformed into a mathematical model with the objective function as follows:

Where:
- ∑ is covariance matrix of returns.
- ω₀ is the last position, i.e., the weight of the last individual stock weight.
- CT is coefficient for turnover costs.
- λ is coefficient for risk aversion.
The constraints include:

3.2.2 Reformulating Objective Function and Constraints
To solve this problem using SOCP, both the objective function and constraints need to be reformulated into an SOCP standard form.
Objective function
Introduce auxiliary variables 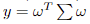 for quadratic terms and
for quadratic terms and ![]() for absolute value terms in turnover constraints. The
objective function can be reformulated as follows:
for absolute value terms in turnover constraints. The
objective function can be reformulated as follows:
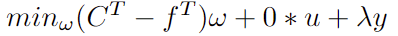
Linear Constraints
The first six linear constraints are similar to those in the previous case and will not be repeated here.
Turnover Constraint
The turnover constraint, involving absolute values (1-norm), is reformulated using auxiliary variable u to fit SOCP format.
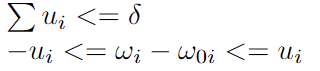
Tracking Error Constraint
The tracking error constraint is a quadratic inequality constraint that can be reformulated using the Cholesky decomposition:
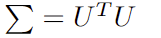
Thus, the original constraint can be transformed into the following SOCP form (specific steps can be referenced in Section 2.2):
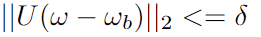
3.2.3 Defining Parameters
Below are the steps to define the parameters:
Coefficient vector of the objective function (f): New variables are introduced for the objective function.
// minimize f^T * w + 0 * u + lamda*y
c = f // coefficients for w
c.append!(take(0, N)) // 0 * u
c.append!(take(lamda, 1)) // lamda*yCoefficient matrix for cone constraints (G):
E = eye(N)// N refers to the number of w
zeros = matrix(DOUBLE, N, N, ,0)// auxiliary variables u
// linear inequality constraints
G = concatMatrix([E,zeros]) // w<=wmax
G = concatMatrix([G, concatMatrix([-E,zeros])], false) // -w <= -wmin
G = concatMatrix([G, concatMatrix([ -wb_one, matrix(DOUBLE,1,N,,0) ] ) ], false) // -w*wb_one <= -w_bmin
G = concatMatrix([G, concatMatrix([ X, matrix(DOUBLE,1,N,,0) ])], false) // Xw <= xn+Xwb, deviation for component stock
G = concatMatrix([G, concatMatrix([-X, matrix(DOUBLE,1,N,,0)])], false) // -Xw <= -x1+Xwb
G = concatMatrix([G, concatMatrix([H, zeros ] ) ], false) // Hw <= hn+Hwb, market capitalization
G = concatMatrix([G, concatMatrix([-H, zeros ])], false) // -Hw <= -h1+Hwb
G = concatMatrix([G, concatMatrix([F, matrix(DOUBLE,1,N,,0)])], false) // F<= fn+Fwb, industry weight
G = concatMatrix([G, concatMatrix([-F, matrix(DOUBLE,1,N,,0)])], false) // -Fw <= -f1+wb
// turnover Constraint
G = concatMatrix([G, concatMatrix([ matrix(DOUBLE,1,N,,0), matrix(DOUBLE,1,N,,1) ] ) ], false) // sum( u_i ) <= delta
G = concatMatrix([G, concatMatrix([E,-E])], false) // w_i -u_i <= w`_i
G = concatMatrix([G, concatMatrix([-E,-E])], false) // -w_i-u_i <= -w`_i
G = concatMatrix([G, concatMatrix([matrix(DOUBLE,1,N,,0), matrix(DOUBLE,1,N,,0)])], false) // || Uw - Uwb ||2 <= delta delta=0.5
G = concatMatrix([G, concatMatrix([-UT, Z]) ], false) // UT is the covariance matrix after Cholesky decomposition
// add the coefficients for the auxiliary variable y
GZ = matrix(DOUBLE, G.shape()[0], 1, , 0)
G = concatMatrix([G, GZ])
// the second-order cone coefficient matrix for the auxiliary variable y
GY = concatMatrix([ matrix(DOUBLE, 1, N, , 0) , matrix(DOUBLE, 1, N, , 0) ])
G = concatMatrix([G, concatMatrix([GY, matrix([-1]) ] ) ], false) // || [2Uw, -y] +[0 , 1] ||2 <= y + 1 y
ZY = matrix(DOUBLE, U.shape()[0], N, , 0)
GY = concatMatrix([2*U, ZY ])
G = concatMatrix([G, concatMatrix([GY, matrix(DOUBLE, U.shape()[0], 1, , 0) ])], false) // || [2Uw, -y] +[0 , 1] ||2 <= y + 1 2U
GY = concatMatrix([matrix(DOUBLE,1,N,,0), matrix(DOUBLE,1,N,,0)])
G = concatMatrix([G, concatMatrix([GY, matrix([1]) ] ) ], false) // || [2Uw, -y] +[0 , 1] ||2 <= y + 1 -yRight-hand-side vector for cone constraints (h) and dimension of non-negative orthant constraints (l):
// linear constrains
h = array(DOUBLE).append!(take(w_max, N)) // w<=w_max
h.append!(take(-wmin, N)) // -w <= -w_min
h.append!(-w_bmin) // -w*wb_one <= -w_bmin
temp = -X[N-1]+X**wb
h.append!(temp[0]) // Xw <= X[0]+X*wb
temp = -X[0]+X**wb
h.append!(-temp[0]) // -Xw <= xn+Xwb
temp = -H[,N-1]+H**wb
temp = exec * from table(temp)
h.append!( temp ) // Hw <= hn+Hwb
temp = -H[,0]+H**wb
temp = exec * from table(temp)
h.append!(-temp) // -Hw <= -h1+Hwb
temp = -F[N-1]+F**wb
h.append!(temp[0]) // F<= fn+Fwb
temp = -F[0]+F**wb
h.append!(-temp[0]) // -Fw <= -f1+wb
h.append!(delta)
h.append!(w0)
h.append!(-w0)
l = h.size()
// quadratic constraints
h.append!(delta)
temp = exec * from table(U**wb)
h.append!(temp)
h.append!(take(1, 1)) //|| [2Uw, -y] +[0 , 1] ||2 <= y + 1
h.append!(take(0, N)) //|| [2Uw, -y] +[0 , 1] ||2 <= y + 1
h.append!(take(1, 1)) //|| [2Uw, -y] +[0 , 1] ||2 <= y + 1 Dimension size of second-order cone constraints (q):
q = [ U.shape()[0]+1, U.shape()[0]+1+1 ]Coefficient matrix and right-hand-side vector for equality constraints (Aeq and beq):
temp = concatMatrix([matrix(DOUBLE, 1, N, ,1), matrix(DOUBLE, 1, N, ,0)])
Aeq = concatMatrix([ temp , matrix(DOUBLE, 1, 1, ,0)])
beq = array(DOUBLE).append!(1)3.2.4 Solving the Optimization Problem
Invoke the socp function with the defined parameters:
res = socp(c, G, h, l, q, Aeq, beq)4. Summary
The socp function is the most commonly used optimization solver
function in DolphinDB. Many complex convex optimization problems can be solved by
reformulating them into SOCP form. Due to well-developed algorithmic solutions for
SOCP, the function delivers superior computational performance, particularly when
solving large-scale optimization problems.
