bondYield

bondYield(settlement, maturity, coupon, price, redemption, frequency, [basis=1], [method='newton'], [maxIter])

settlement is a DATE scalar or vector indicating the settlement date.

maturity is a DATE scalar or vector indicating the maturity date.

coupon is a numeric scalar or vector indicating the annual coupon rate.

price is a numeric scalar or vector of the same length as settlement indicating the bond price per 100 face value.

redemption is a numeric scalar or vector indicating the redemption value per 100 face value.

frequency (optional) is an INT scalar/vector indicating the number of payments, or a DURATION scalar/vector indicating payment frequency. This parameter is required when bondType is 0 or unspecified. It can be:

• 1/1y: Annual payments
• 2/6M: Semi-annual payments
• 4/3M: Quarterly payments
• 12/1M: Monthly payments

method (optional) is a STRING scalar or vector indicating the optimization algorithm used to solve the bond yield. It can be:

• "newton" (default): Newton algorithm.
• "brent": Brent algorithm.
• "nm": Nelder-Mead simplex algorithm.
• "bfgs": BFGS algorithm.
• "lbfgs": LBFGS algorithm.

maxIter (optional) is a positive integer or a vector of positive integers indicating the maximum number of iterations. The default value is 100.

Calculate the bond yield for each 100 face value of a bond based on its price.

Return value: A DOUBLE scalar or vector.

Note:

• If there is one coupon period or less until redemption, YIELD is calculated as follows:
  
  
  
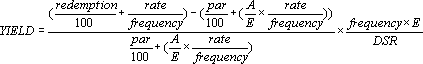
  where:
  • • A = number of days from the beginning of the coupon period to the settlement date (accrued days).
    • DSR = number of days from the settlement date to the redemption date.
    • E = number of days in the coupon period.

• If there is more than one coupon period until redemption, bond yield is calculated through a hundred iterations. The resolution uses the Newton method. The yield is changed until the estimated price given the yield is close to price.

• An annual coupon rate is used by default.

Calculate the yield for a bond issued on January 15, 2008, with a maturity date of November 15, 2016, an annual coupon rate of 5.75%, a redemption price of 100, semi-annual interest payments, and a US (NASD) 30/360 day count basis, using the optimization algorithms 'newton', 'nm', 'brentq', 'bfgs', and 'lbfgs'.

settlement = 2008.02.15
maturity = 2016.11.15
coupon = 0.0575
price = 95.04287
redemption = 100
frequency = 2
basis = 0
method = ['newton', 'nm', 'brentq', 'bfgs','lbfgs']
bondYield(settlement, maturity, coupon, price, redemption, frequency, basis, method)
// Output:[0.065000006880755,0.064999847412109,0.065000006880759,0.064999999976412,0.065000004967984]