Precision and Accuracy in DECIMAL Calculations
1. Characteristics of DECIMAL Calculations
1.1. Calculation Logic
In DolphinDB, a DECIMAL value is divided into two parts for storage: a raw integer containing the raw data, and a scale denoting the number of decimal places. For example, the decimal value 1.23 with a precision of 2 decimal places would be stored as the raw integer 123 and the scale: 2. This storage approach allows calculations to be performed directly on the integer data to avoid precision loss.
When calculating DECIMAL values with functions that return Floating results, calculations are first performed on the integers. The eventual result is converted to Floating type to avoid precision loss during calculation. For example, when calculating the average of DECIMAL32(2) values [1.11, 2.22, 3.33], DolphinDB first computes the sum of the integers 111 + 222 + 333 = 666, and then converts the result to DOUBLE type and divides by the count double(666) / 10^2 / 3 = 2.22.
For the rules of DECIMAL arithmetic operations, see DECIMAL Data Type.
1.2. Data Types of Results
This section discusses the return types when a computational function takes DECIMAL values as inputs.
Only the following DDB functions take DECIMAL inputs and also return DECIMAL results to retain the full decimal precision throughout: sum, max, min, first, last, firstNot, lastNot, and their corresponding cum, m, tm and TopN functions, as well as cumPositiveStreak.
a = decimal64(rand(10,100),4)
typestr(sum(a))
// output: DECIMAL128
typestr(cummax(a))
// output: FAST DECIMAL64 VECTOR
typestr(mmin(a,5))
// output: FAST DECIMAL64 VECTOR
T = 2023.03.23..2023.06.30
typestr(tmsum(T, a, 3))
// output: FAST DECIMAL128 VECTOR
typestr(cumPositiveStreak(a))
// output: FAST DECIMAL128 VECTORNote that DECIMAL128 is introduced since version 2.00.10, and the input and output of sum-related functions (including sum/cumsum/msum/tmsum/msumTopN/cumsumTopN/tmsumTopN/cumPositiveStreak) are as follows:
| Input Type | Output Type |
|---|---|
| DECIMAL32 | DECIMAL64 |
| DECIMAL64 | DECIMAL128 |
| DECIMAL128 | DECIMAL128 |
Except the functions listed above, functions such as avg, std, var, and skew, and their corresponding cum, m, tm, TopN functions, take DECIMAL inputs and return DOUBLE results.
a = decimal64(rand(10,100),4)
typestr(avg(a))
// output: DOUBLE
typestr(cumstd(a))
// output: FAST DOUBLE VECTOR
typestr(mvar(a,5))
// output: FAST DOUBLE VECTOR
T = 2023.03.23..2023.06.30
typestr(tmskew(T, a, 3))
// output: FAST DOUBLE VECTORThe following table lists the output data types when calculating DECIMAL64 data:
| Function | Input Type | Output Type |
|---|---|---|
| sum/cumsum/msum/tmsum | DECIMAL64 | DECIMAL128 |
| msumTopN/cumsumTopN/tmsumTopN | DECIMAL64 | DECIMAL128 |
| max/cummax/mmax/tmmax | DECIMAL64 | DECIMAL64 |
| min/cummin/mmin/tmmin | DECIMAL64 | DECIMAL64 |
| first/mfirst/tmfirst | DECIMAL64 | DECIMAL64 |
| last/mlast/tmlast | DECIMAL64 | DECIMAL64 |
| firstNot/cumfirstNot | DECIMAL64 | DECIMAL64 |
| lastNot/cumlastNot | DECIMAL64 | DECIMAL64 |
| cumPositiveStreak | DECIMAL64 | DECIMAL128 |
| avg/cumavg/mavg/tmavg/mavgTopN/cumavgTopN/tmavgTopN | DECIMAL64 | DOUBLE |
| sum2/cumsum2/msum2/tmsum2 | DECIMAL64 | DOUBLE |
| prod/cumprod/mprod/tmprod | DECIMAL64 | DOUBLE |
| med/cummed/mmed/tmmed | DECIMAL64 | DOUBLE |
| std/cumstd/mstd/tmstd/mstdTopN/cumstdTopN/tmstdTopN | DECIMAL64 | DOUBLE |
| skew/mskew/tmskew/mskewTopN/cumskewTopN/tmskewTopN | DECIMAL64 | DOUBLE |
| kurtosis/mkurtosis/tmkurtosis/mkurtosisTopN/cumkurtosisTopN/tmkurtosisTopN | DECIMAL64 | DOUBLE |
| corr/cumcorr/mcorr/tmcorr/mcorrTopN/cumcorrTopN/tmcorrTopN | DECIMAL64 | DOUBLE |
| covar/cumcovar/mcovar/tmcovar/mcovarTopN/cumcovarTopN/tmcovarTopN | DECIMAL64 | DOUBLE |
| beta/cumbeta/mbeta/tmbeta/mbetaTopN/cumbetaTopN/tmbetaTopN | DECIMAL64 | DOUBLE |
2. Performance and Accuracy Tradeoffs
2.1. Advantages of DECIMAL
Floating numbers have inherent limitations in accurately representing real values in computer systems. This stems from two main reasons. First, binary floating-point formats can only approximate decimal values that have finite representations, such as 0.1. The binary representation cannot precisely encode such decimal fractions. Second, Floating types have a finite range and precision. If a number exceeds the maximum or minimum representable value, the computer system will round or truncate it, introducing further imprecision. In contrast, the DECIMAL data type is capable of precisely representing and computing with data that has an exact decimal representation.
For example, the Floating type is unable to precisely represent the value 123.0001, whereas the DECIMAL type can accurately represent it.
a =123.0001
print(a)
// output: 123.000100000000003
b = decimal64(`123.0001,15)
print(b)
// output: 123.000100000000000Calculating avg of Floating numbers may yield precision errors, whereas DECIMAL returns an accurate result of DOUBLE type.
a = array(DOUBLE,0)
for (i in 1..100){
a.append!(123.0000+0.0003*i)
}
avg(a)
// output: 123.015149999999
avg(a) == 123.01515
// output: false
eqFloat(avg(a),123.01515)
// output: true
b= array(DECIMAL64(4),0)
for (i in 1..100){
b.append!(123.0000+0.0003*i)
}
avg(b)
// output: 123.015150000000
typestr(avg(b))
// output: DOUBLE
avg(b) == 123.01515
// output: true2.2. Disadvantages of DECIMAL
Overflow Issues
The numeric ranges for the DECIMAL32/DECIMAL64/DECIMAL128 types are as shown in the table below, where S designates the preserved decimal digits.
| Underlying Storage Data Types | Byte Size | Scale Range | Valid Numeric Range | Maximum Number of Digits | |
|---|---|---|---|---|---|
| DECIMAL32 | int32_t | 4 | [0,9] | (-1 * 10 (9 - S), 1 * 10 (9 - S)) | 9 |
| DECIMAL64 | int64_t | 8 | [0,18] | (-1 * 10 (18 - S), 1 * 10 (18 - S)) | 18 |
| DECIMAL128 | int128_t | 16 | [0,38] | (-1 * 10 (38 - S), 1 * 10 (38 - S)) | 38 |
DECIMAL values may encounter overflow issues constrained by the valid numeric range and maximum number of digits. As of version 2.00.10, DolphinDB supports automatic conversion to a higher precision DECIMAL type to avoid overflow in arithmetic operations:
version 2.00.9.6:
a = decimal32(4.0000,4)
b = decimal32(8.0000,4)
c = a*b
// Server response: 'c = a * b => Decimal math overflow'
version 2.00.10:
a = decimal32(4.0000,4)
b = decimal32(8.0000,4)
c = a*b
print(c)
// output: 32.00000000
typestr(c)
// output: DECIMAL64However, there still remains overflow risks with DECIMAL128:
a = decimal128(36.00000000,8)
b = a*a*a*a
// Server response: 'b = a * a * a * a => Decimal math overflow'As shown in the above example, when multiplying two DECIMAL values in DolphinDB, the result scale is determined by summing the operand scales. This can lead to an overflow error if the number of digits exceeds the DECIMAL precision limit. In the case of variable "b", the expected result is 1679616.00000000000000000000000000000000, which contains 39 digits. This exceeds the maximum representation of 38 digits for DECIMAL128 and leads to an overflow.
As of version 2.00.10, the decimalMultiply function is introduced for DECIMAL multiplication. Compared with the multiply function (and * operator), this function allows specifying the precision of result. In cases where multiplying DECIMAL values could lead to overflow due to accumulated scales, decimalMultiply can be used to set the result precision explicitly and avoid overflow.
a = decimal64(36.00000000,8) decimalMultiply(a, a, 8)
// output: 1296.00000000Conversion Errors
If we generate DECIMAL values from constants, errors might occur due to the conversion of floating-point numbers:
a = 0.5599
decimal64(a, 4)
// output: 0.5598To mitigate such errors, using strings to generate DECIMAL types is recommended:
a = "0.5599"
decimal64(a, 4)
// output: 0.5599Memory Usage
DECIMAL32, DECIMAL64, and DECIMAL128 types occupy 4 bytes, 8 bytes, and 16 bytes of memory. FLOAT and DOUBLE types use 4 bytes and 8 bytes. DECIMAL128 could take up twice the memory of DOUBLE to represent the same value. Additionally, arithmetic overflows in DECIMAL32 and DECIMAL 64 that trigger type promotion may double the memory usage. This can pose a potential memory risk when working with large datasets of DECIMAL type.
Computing Performance
Compared to FLOAT and DOUBLE types, calculations of DECIMAL are slower due to the more complex internal representation. Specific performance comparisons will be presented in the next chapter.
Limitations
Currently, the DECIMAL type in DolphinDB has fewer functions and less compatibility than FLOAT/DOUBLE:
- Some computational functions do not yet support DECIMAL data types.
- Most statistical functions will generate Floating results even when taking DECIMAL numbers as inputs.
- Matrices and sets do not support DECIMAL data types.
- For data type conversion, the DolphinDB system currently does not support the conversion between DECIMAL types and BOOL/CHAR/SYMBOL/UUID/IPADDR/INT128 types or temporal types. To convert STRING or BLOB type to DECIMAL, the string must be convertible to a numeric type.
3. Floating v.s. DECIMAL: Performance Comparison
To evaluate the computational performance of Floating and DECIMAL types, the following example uses several commonly-used computational functions and measures the computation time for each data type using the same dataset.
First, execute the following script to simulate data:
n = 1000000
data1 = rand(float(100.0), n)
data2 = double(data1)
data3 = decimal32(data1, 4)
data4 = decimal64(data1, 4)
data5 = decimal128(data1, 4)The timer statement is used to measure the computation time:
timer(100) { sum(data1) } // Executing 100 times to lower single computation errors and magnify differences in time consumption between different types
timer(100) { sum(data2) }
timer(100) { sum(data3) }
timer(100) { sum(data4) }
timer(100) { sum(data5) }
...Below is the computation time (in ms) for each function and data type:
| Function | FLOAT | DOUBLE | DECIMAL32 | DECIMAL64 | DECIMAL128 |
|---|---|---|---|---|---|
sum | 52.985 | 64.331 | 28.721 | 57.234 | 107.126 |
sum2 | 173.278 | 211.772 | 176.261 | 180.051 | 603.422 |
prod | 63.650 | 55.641 | 171.718 | 174.389 | 18850.009 |
avg | 178.086 | 210.495 | 26.094 | 106.869 | 258.508 |
std | 362.388 | 345.758 | 278.933 | 319.177 | 968.276 |
kurtosis | 547.751 | 407.561 | 585.859 | 769.879 | 1013.591 |
skew | 546.705 | 439.348 | 622.758 | 842.994 | 1074.128 |
The performance statistics reveal the performance differences when calculating Floating and DECIMAL values in DolphinDB:
(1) For most of the computational functions, computing DECIMAL is slower than FLOAT/DOUBLE types.
(2) During computations, DECIMAL128 is converted into LONG DOUBLE (and DECIMAL32/DECIMAL64 into DOUBLE). A LONG DOUBLE can take up 12 or 16 bytes, depending on the compiler and CPU. Multiplying LONG DOUBLE values can be highly time-consuming when dealing with huge volume of data. In the given example, the values of the vectors are relatively large, resulting in large products and slower calculations. However, when working with smaller value ranges like [0.5, 1.0], the calculation speed of DECIMAL128 is more comparable to that of DECIMAL32/64.
(3) When conducting calculations with DECIMAL types, certain functions exhibit minimal performance differences compared to Floating numbers. DECIMAL32/64 can even achieve performance comparable to or even better than FLOAT/DOUBLE. This is because DECIMAL computations essentially operate on raw integers, allowing results to be returned directly as DECIMAL or converted to Floating types. Additionally, operations on Floating data (such as sum) may involve loop unrolling and consequently take more time during calculations.
4. Best Practice for Calculating DECIMAL: mavg
In this chapter, the precision of calculations in DECIMAL and Floating types is measured, with a specific focus on the precision loss that occurs during calculations such as moving average.
DolphinDB provides two methods for calculating moving average: mavg and moving(avg, ...). However, the calculation logic differs. The mavg algorithm involves adding new values to the window and subtracting unneeded values while calculating the average. This process introduces precision issues due to the addition and subtraction operations. On the other hand, moving(avg, ...) calculates the average of all the elements every time when a window is determined.
First, import test data from tick.csv (with data of DOUBLE type), and calculate mavg and moving(avg, ...):
data = loadText("<yourDirectory>/tick.csv")
t = select
MDTime,
((LastPx - prev(LastPx)) / (prev(LastPx) + 1E-10) * 1000) as val,
mavg(((LastPx - prev(LastPx)) / (prev(LastPx) + 1E-10) * 1000), 20, 1),
moving(avg, ((LastPx - prev(LastPx)) / (prev(LastPx) + 1E-10) * 1000), 20, 1)
from dataThe result is as shown below. Calculation errors start to appear between the two methods from 09:31:53.000 onwards.
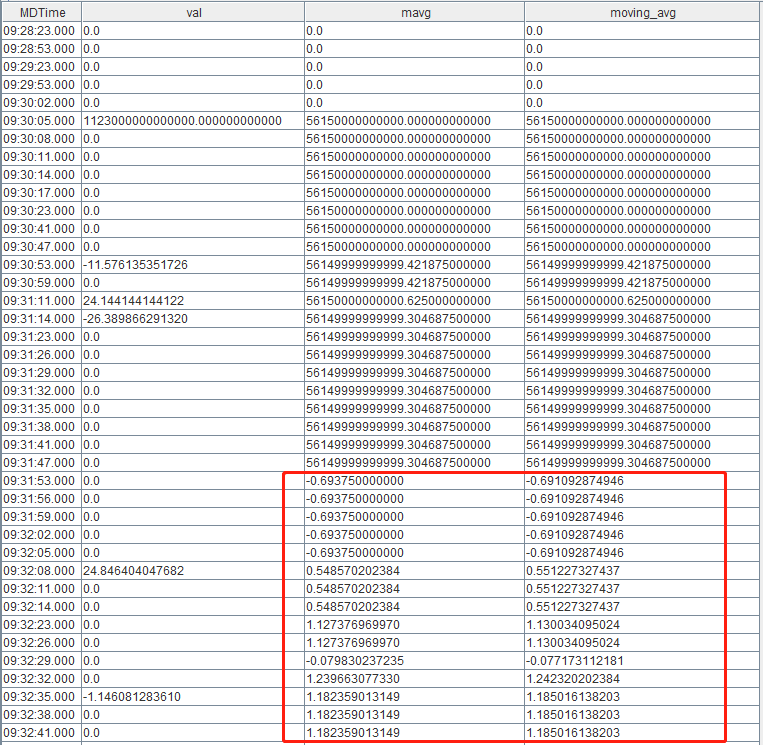
To mitigate these calculation errors, the following script converts the intermediate calculation results to DECIMAL128 type before invoking mavg and moving(avg, ...):
data = loadText("<yourDirectory>/tick.csv")
t = select
MDTime,
((LastPx - prev(LastPx)) / (prev(LastPx) + 1E-10) * 1000) as val,
mavg(decimal128(((LastPx - prev(LastPx)) / (prev(LastPx) + 1E-10) * 1000), 4), 20, 1),
moving(avg, decimal128(((LastPx - prev(LastPx)) / (prev(LastPx) + 1E-10) * 1000), 4), 20, 1)
from dataThe result is as shown below:
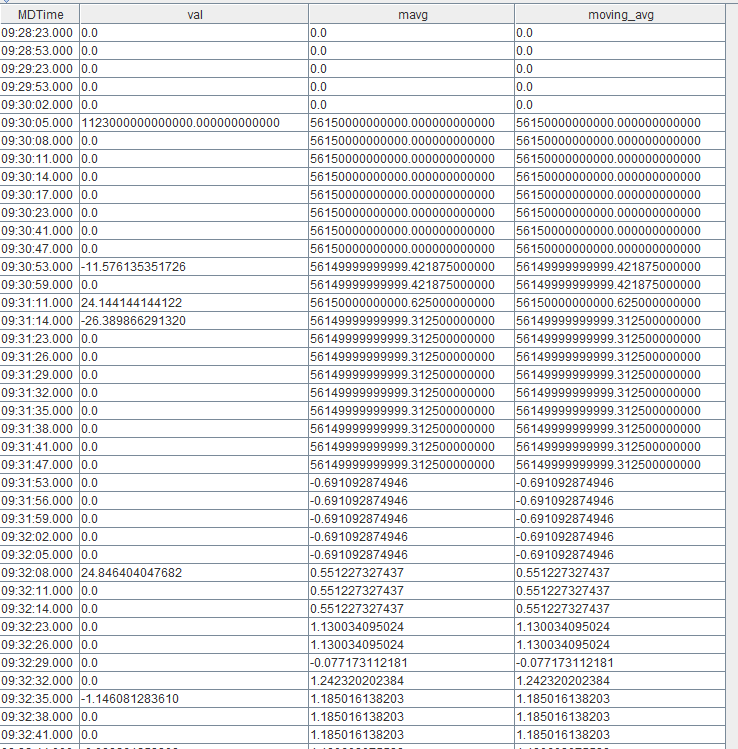
As observed, the results of mavg and moving(avg, ...) are identical.
Functions like avg and std, and their corresponding cum, tm, m, TopN functions, may encounter precision errors in computations due to the precision issues in floating-point calculations. In situations where precision is important, it is recommended to use DECIMAL for calculations.
5. Conclusion
Floating-point representations can introduce small errors and imprecise values due to their internal binary storage. The DECIMAL data types in DolphinDB provide accurate representations to avoid these precision issues. However, using DECIMAL comes with drawbacks such as potential overflow, higher memory usage, and relatively lower performance. Despite these limitations, in certain scenarios, using the DECIMAL types can effectively prevent discrepancies between expected and computed outcomes. In summary, DECIMAL types provide accurate representations at the potential expense of performance and scalability.
