osqp
Syntax
osqp(q, [P], [A], [lb], [ub])
Parameters
q is a vector indicating the linear coefficient of the objective function.
P (optional) is a positive semi-definite matrix indicating the quadratic coefficients of the objective function.
A (optional) is the coefficient matrix of linear inequality constraints.
lb (optional) is the left-hand-side vector of the linear inequality constraint.
ub (optional) is the right-hand-side vector of the linear inequality constraint.
A, lb, and ub must be all specified or not.
lb and ub can contain null values, but their length must match the number of rows in A. Null values in ub and lb are treated as positive/negative infinity and take ±1030 during computation.
Details
Solve the following optimization problem with a quadratic objective function and a set of linear constraints.
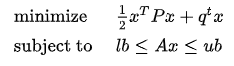
Return value: A 2-element tuple:
-
The first element is a string indicating the state of the solution:
-
solved: solution found;
-
solved inaccurate: solution found but the result is inaccurate;
-
primal infeasible: no feasible solution to the primal;
-
dual infeasible: no feasible solution to the dual;
-
maximum iterations reached: reach the maximum number of iterations;
-
run time limit reached: execution timeout;
-
problem non convex: the problem is non-convex;
-
interrupted: solution interrupted;
-
unsolved: solution not found.
-
-
The second element is the value of x where the value of the objective function is minimized.
Examples
P = matrix(4e-2 6e-3 -4e-3 0.0, 6e-3 1e-2 0.0 0.0, -4e-3 0.0 2.5e-3 0.0, 0.0 0.0 0.0 0.0)
q = [-2, -4, 2, 3]
A = [1,2,1,1,3,-1,2,1,3,1,-1,1,-2,-4,-5,1]$4:4
l = [,,,1.0]
u = [3.0,2.0,-1.0,1.0]
res = osqp(q, P, A, l, u)
// output: ("solved",[-64.364818313795097,368.910318139716082,-548.041799338347459,244.496302999333039])