Moving TopN Functions (mTopN functions)

• Higher-order function aggrTopN:

  aggrTopN(func, funcArgs, sortingCol, top, [ascending=true])

• Syntax templates for mTopN functions:

  mTopN(X, S, window, top, [ascending=true], [tiesMethod])
  mTopN(X, Y, S, window, top, [ascending=true], [tiesMethod])

  Parameters:

  X (Y) is a numeric vector or matrix.

  S is a numeric/temporal vector or matrix, based on which X are sorted.

  window is an integer greater than 1, indicating the sliding window size.

  top is an integer in (1, window], indicating the first top elements of X after sorted based on S.

  ascending (optional) is a Boolean value indicating whether to sort S in ascending order. The default value is true.

  tiesMethod (optional) is a string that specifies how to select elements if there are more elements with the same value than spots available in the top N after sorting X within a sliding window. It can be:

  • 'oldest': select elements starting from the earliest entry into the window;

  • 'latest': select elements starting from the latest entry into the window;

  • 'all': select all elements.

  Note: For backward compatibility, the default value of tiesMethod is 'oldest' for the following functions: mstdTopN, mstdpTopN, mvarTopN, mvarpTopN, msumTopN, mavgTopN, mwsumTopN, mbetaTopN, mcorrTopN, mcovarTopN; For the remaining mTopN functions, the default value of tiesMethod is 'latest'.

• mTopN(X, S, window, top, [ascending=true], [tiesMethod])

  msumTopN, mavgTopN, mstdTopN, mstdpTopN, mvarTopN, mvarpTopN, mskewTopN, mkurtosisTopN, mpercentileTopN

• mTopN(X, Y, S, window, top, [ascending=true], [tiesMethod])

  mwsumTopN, mbetaTopN, mcorrTopN, mcovarTopN

Within a sliding window of given length (measured by the number of elements), the function stably sorts X (or X, Y) by S in the order specified by ascending, then obtains the first top elements for calculation.

Note: NULL values in S are ignored in data sorting.

The following example uses function msumTopN:

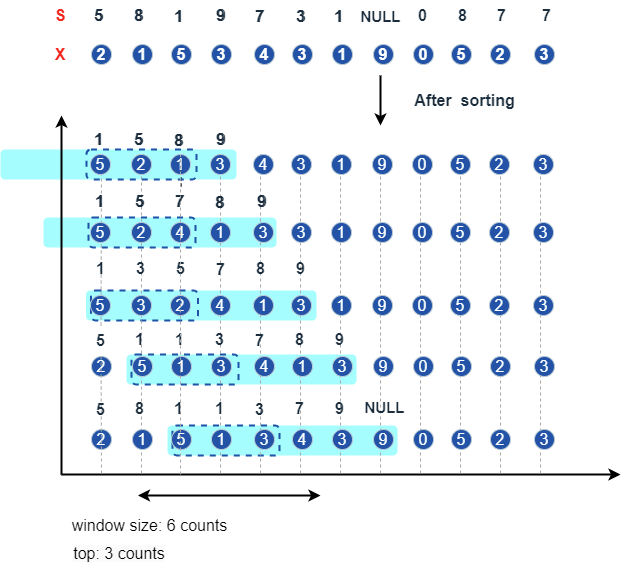
X = [2, 1, 5, 3, 4, 3, 1, 9, 0, 5, 2, 3]
S = [5, 8, 1, 9, 7, 3, 1, NULL, 0, 8, 7, 7]

msumTopN(X, S, window=6, top=3)
// output
[2,3,8,8,11,10,9,9,4,4,4,3]

In the following figure, the elements of X are sorted based on S in ascending order in a sliding window of length 6, and the first 3 elements are selected for calculation. For the first top windows, all the elements are taken for calculation. Therefore, the figure illustrates the rules starting from the top + 1 window.

The following examples show the usage of parameter tiesMethod:

X = [2, 1, 4, 3, 4, 3, 1]
S = [5, 8, 1, 1, 1, 3, 1]
// For the last window, there are four elements of value 1
// As tiesMethod is not specified, the default 'oldest' is used, meaning the first 3 occurrences of 1 (corresponding to 4, 3, 4 of X) are selected
msumTopN(X, S, window=6, top=3)
// output
[2,3,7,9,11,11,11]

// As tiesMethod is set to 'latest', the latest 3 occurrences of 1 (corresponding to 3, 4, 1 of X) are selected
msumTopN(X, S, window=6, top=3, tiesMethod=`latest)
// output
[2,3,7,9,11,11,8]

// As tiesMethod is set to 'all', all the occurrences of 1 (corresponding to 4, 3, 4, 1 of X) are selected
msumTopN(X, S, window=6, top=3, tiesMethod=`all)
// output
[2,3,7,9,11,11,12]