socp
Syntax
socp(f, [G], [h], [l], [q], [A], [b])
Details
Solve SOCP problems and calculate the minimum of the objective function under specified constraints. The standard form of the SOCP constraint is as follows:
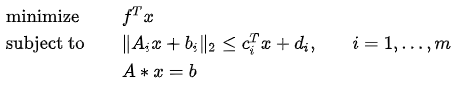
G is as follows:
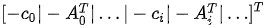
h is as follows:
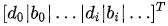
Arguments
Second-order cone programming (SOCP) problems are subject to the constraint with the following form:
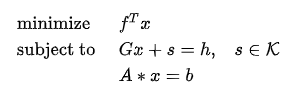
K is a cone and s is a slack variable. The value of s will be determined during optimization.
f is a numeric vector indicating the coefficient vector of the objective function.
G (optional) is a numeric matrix indicating the coefficient matrix of the cone constraint.
h (optional) is a numeric vector indicating the right-hand-side vector of the cone constraint.
l (optional) is an integral scalar indicating the dimension of the non-negative quadrant constraint.
q (optional) is a positive vector indicating the dimension size of each second-order cone constraint. The form is [r0,r1,…,rN-1].
A (optional) is a numeric matrix indicating the coefficient matrix of the equality constraint.
b (optional) is a numeric vector indicating the right-hand-side vector of the equality constraint.
Return value
A 4-element tuple:
- The first element is a string indicating the state of the solution:
- The second element is the value of x where the value of the objective function is minimized.
- The third element is the minimum value of the objective function.
- The fourth element is the exit code that indicates the quality of the returned solution.
The correspondence between Exicode and status descriptions is shown in the following table:
| Exitcode | Description |
|---|---|
| 0 | Optimal solution found |
| 1 | Certificate of primal infeasibility found |
| 2 | Certificate of dual infeasibility found |
| 10 | Optimal solution found subject to reduced tolerances |
| 11 | Certificate of primal infeasibility found subject to reduced tolerances |
| 12 | Certificate of dual infeasibility found subject to reduced tolerances |
| -1 | Maximum number of iterations reached |
| -2 | Numerical problems (unreliable search direction) |
| -3 | Numerical problems (slacks or multipliers outside cone) |
| -7 | Unknown problem in solver |
Examples
Solve the following SOCP problem:
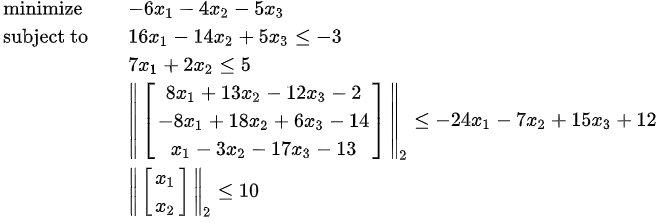
f = [-6, -4, -5]
G = matrix([[16, 7, 24, -8, 8, -1, 0, -1, 0],
[-14, 2, 7, -13, -18, 3, 0, 0, -1],
[5, 0, -15, 12, -6, 17, 0, 0, 0]])
h = [-3, 5, 12, -2, -14, -13, 10, 0, 0]
l = 2
q = [4,3]
re = socp(f,G,h,l,q, ,)
print(re)
// output: ("Optimal solution found",[-9.902804882871327,-1.39084684264198,26.211851780740154],-66.079042235904907,0)